Existen diferentes maneras de elegir a un representante popular con base en las preferencias electorales de los votantes. En este artículo mostramos varios métodos que se pueden aplicar para este propósito; aunque, cada uno de ellos puede arrojar un resultado distinto, dada la distribución de votos.

Lo que este ejercicio muestra es que diferentes métodos de acumulación de preferencias producen resultados distintos, y es tarea del poder legislativo determinar cuál es el más conveniente para un país.

Supongamos que tenemos cuatro candidatos A, B, C y D, y que cada votante les asigna una preferencia con un número, del 1 al 4. Ahora imaginemos que de esas asignaciones emergen cuatro secuencias preferidas por cierto número de votantes, como se muestra en la Tabla 1.

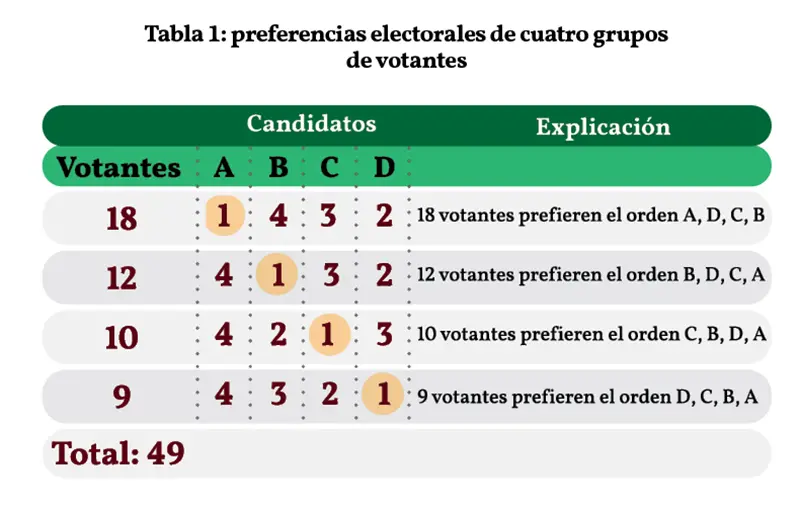
A observar, 18 votantes dan el primer lugar de preferencia para “A”; 12 prefieren a “B”; 10 eligieron a “C”; y 9 escogieron a “D”. Los 18 votantes que prefieren a A, le asignan al partido B el cuarto lugar, a C el tercero y a D el segundo lugar de sus preferencias. Así es como hay que leer la tabla.

Voto por mayoría relativa: gana el candidato A

Supongamos que se realiza la elección y los ciudadanos votan por los candidatos de su primera preferencia. En ese caso, el candidato A obtiene 18 votos, que es más de lo que cualquier otro candidato puede recibir, y por eso gana la elección por mayoría relativa. Pero observemos que A es, al mismo tiempo, muy poco popular con el resto de los electores (que son 31), porque lo ubican en el cuarto lugar de sus preferencias electorales. Aunque A es un candidato que puede atraer 18 de 49 votos (37%) es un candidato polarizador. Si A es el triunfador, 31 votantes quedan muy insatisfechos.

Voto por segunda vuelta: gana el candidato B

Si la elección se realiza a dos vueltas, en la primera vuelta gana A, pero sin más del 50% de los 49 votos emitidos. En ese caso hay que ir a una segunda vuelta, en donde se enfrentan los candidatos A y B, por haber sido los que recibieron más votos.

En la segunda vuelta, dado que A es muy impopular entre los candidatos que prefieren a B, C y D, no va a obtener más de los 18 votos que ya tenía. El candidato B, por el contrario, es mejor visto que A por los partidarios de C y D (cuyos candidatos ya no toman parte en la segunda vuelta), así que B recibe 12+10+9 votos, es decir, 31 en total, y así gana la segunda vuelta.

Diferentes métodos de acumulación de preferencias producen resultados distintos.

Voto considerando primero y segundo lugar de preferencia: gana el candidato D

Dado que considerando solo la primera preferencia ningún candidato alcanza 50% de los votos, se pueden sumar los votos de la primera y segunda preferencia para ver qué ocurre. Si hacemos esto tomando la tabla de preferencias como base, vemos que A alcanza 18 votos, B 12+10=22, C obtiene 10+9=19 y D obtiene hasta 18+12+9=39 votos. Eso sucede porque D es la segunda opción de los votantes que prefieren a A y a B. Es decir, 39 votantes pueden estar satisfechos con D, ya sea porque lo prefieren, o porque es su segunda opción. Con 39 votos, D alcanza la mayoría absoluta. Podríamos decir que D es un candidato “moderado” que no polariza a los votantes y por eso gana al sumar las primeras y segundas preferencias.

Voto eliminando candidatos progresivamente: gana el candidato C

Un algoritmo alternativo, llamado “de Hare”, que es muy utilizado en el mundo, consta en ir eliminando a candidatos progresivamente y redistribuir los sufragios que obtuvieron hacia la segunda preferencia (el recuadro al final de este artículo muestra un ejemplo gráfico). 

En la Tabla 1 de votos vemos que D es el candidato con menos preferencias para el primer lugar: sólo 9; entonces, se migran hacia el candidato C, que es la segunda preferencia de los candidatos de D.  La Tabla 2 muestra lo que sucede. Los votos de los votantes que prefieren a cada partido A, B, C y D, en primer lugar, los encontramos en el primer renglón. En el renglón que sigue, vemos cómo los 9 votos del candidato D, que ha sido eliminado, migran hacia el candidato C, la segunda preferencia de los seguidores de D. 

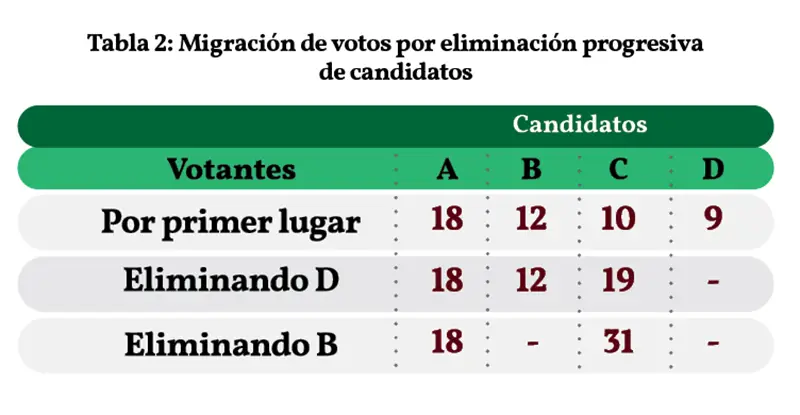
Ahora, sin el candidato D, el candidato con menos votos es B (solo tiene 12). Lo eliminamos y sus votos migran al candidato C, que es la tercera opción de sus partidarios, ya que la segunda opción de ellos (candidato D) ya fue eliminado. Obtenemos el último renglón de la tabla, que cierra la elección, ya que el candidato C alcanza 31 votos, que es mayoría absoluta.

Este método de elección se llama “algoritmo de Hare” o bien “segunda vuelta inmediata”, porque al final, en este ejemplo, solo los candidatos A y C quedan enfrentados, sin tener que hacer una segunda vuelta electoral real. Todo sucede en el papel, tomando en cuenta la lista de preferencias de los electores. Cuando hay muchos candidatos que se van eliminando progresivamente, el primer candidato que obtiene más del 50% de los votos, gana la elección, aunque aún haya más de dos candidatos que no han sido eliminados.

Generalmente, los electores se acostumbran rápidamente al sistema y lo entienden. 

Logística

Una elección a dos vueltas requiere la realización de dos elecciones, usualmente en días diferentes. Una elección de segunda vuelta inmediata (es decir algorítmica) requiere que en las casillas electorales, los representantes realicen los cálculos manualmente (como se hace en Austria), o bien, utilizando máquinas electorales (como se hace en Alaska y San Francisco).

Un punto importante es determinar si los electores se confunden o no al votar. La experiencia de las elecciones en San Francisco, Australia, Austria y otros países, o ciudades donde se ha utilizado la votación por preferencias, es que los electores se acostumbran rápidamente al sistema y lo entienden. 

Los votantes no necesitan asignar una preferencia a todos los candidatos. Si el votante solo les asigna la preferencia 1, 2 y 3 a tres candidatos, en una elección con diez candidatos, el método para contar los votos funciona de la misma manera. El único peligro es que, si los tres candidatos preferidos por este votante son eliminados, entonces el voto de esta persona deja de contar. En ese caso, el votante es indiferente con respecto al resultado si sus tres primeras preferencias no son electas.

En una votación por preferencias, los votantes no necesitan asignar una preferencia a todos los candidatos.

Existen otras variantes de votación por preferencias, como, por ejemplo, ir eliminando de una lista primero a los candidatos más impopulares, pero eso no lo ilustramos aquí. 

El voto por mayoría relativa puede dejar a la mayoría de los votantes insatisfechos. La segunda vuelta es mejor, pero si se fragmentan los votos entre muchos partidos, uno de los dos candidatos que van a la segunda vuelta pudiera llegar ahí aun siendo bastante impopular. Es lo que sucedió en Francia en las elecciones presidenciales de 2002, cuando hubo 16 candidatos y los dos finalistas fueron Jacques Chirac y Jean-Marie Le Pen (con 20% y 17% de los votos, respectivamente). En la segunda vuelta, Chirac ganó con 82% de los votos, ya que por Le Pen solo votaron los extremistas. El método de Hare, que va eliminando a los candidatos más débiles, uno por uno, pero sigue considerando sus preferencias, hubiera llevado en 2002 a una elección entre los dos candidatos más importantes y con más apoyo, Jacques Chirac y Lionel Jospin.

Fuente

Voting and Elections: Election Decision Methods. (2004, octubre). American Mathematical Society. https://www.ams.org/publicoutreach/feature-column/fcarc-voting-decision