En las matemáticas de los griegos, una estrategia de solución de expresiones algebraicas (lo que llamamos ecuaciones) consistía en reducirlas a un problema geométrico equivalente. Si, como un ejemplo muy simple, se quería hallar un valor numérico con cuadrado igual a 16; esto se puede concebir como el equivalente a encontrar la longitud de uno de los lados de un cuadrado cuya área es 16.

Pero hoy en día procedemos más bien al revés: tratamos de reducir problemas geométricos a expresiones algebraicas, es decir, a ecuaciones que podemos resolver aplicando las reglas del álgebra.

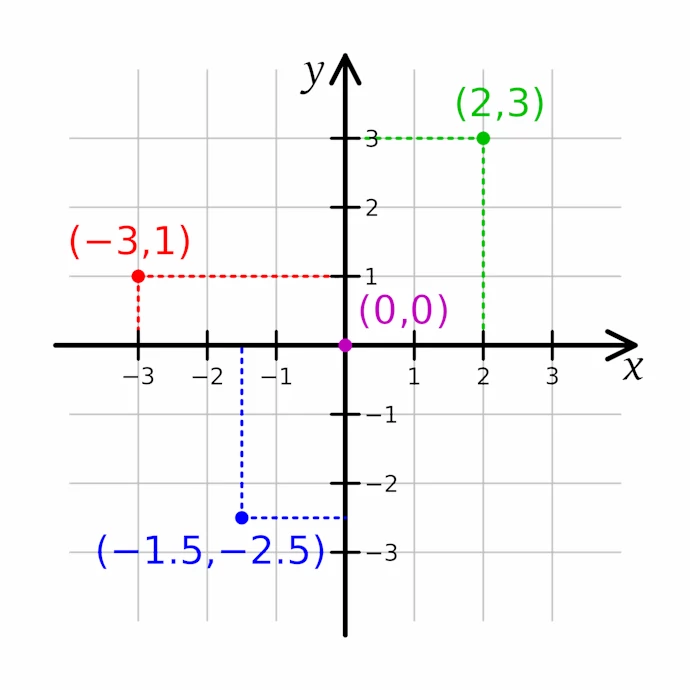
Estamos ya acostumbrados a ver por doquier, en revistas y diarios, diagramas de dos dimensiones. Por ejemplo, curvas que describen el movimiento del mercado de acciones o el crecimiento de la economía a lo largo de los años. Se utilizan para ello las llamadas “coordenadas cartesianas”, como en la figura adjunta. Tenemos un eje horizontal que asociamos con la variable “x” y un eje vertical que asociamos con la variable “y”.

Un punto con coordenadas (2,3) se encuentra a dos unidades del eje horizontal y a tres del eje vertical. Para cada punto en el plano hay un valor único de “x” y uno de “y”. Hacia la izquierda del origen y hacia abajo representamos las distancias a los ejes con números negativos.

A pesar de que esto es ya algo que los niños aprenden en las escuelas, la verdad es que tomó mucho tiempo poder llegar esta representación llamada “cartesiana” en las matemáticas (en honor a René Descartes). Esto es la base de lo que se llama la “geometría analítica”, que nos permite graficar funciones y, lo dicho, convertir problemas geométricos en problemas de álgebra.

La primera asociación matemática entre un punto de una superficie y dos números que lo representan se dio en la cartografía. Puntos sobre la Tierra pueden ser especificados a través de su longitud y latitud. La latitud de Londres es de 51.5 grados y su longitud de sólo 0.12 grados, ya que el meridiano de Greenwich casi pasa por Londres.

Se dice que el filósofo griego Eratóstenes propuso un sistema de latitud y longitud para la cartografía, ya desde el siglo tercero a. C. El meridiano de referencia pasaba por la ciudad de Alejandría, mientras que las líneas de latitud pasaban por ciudades conocidas.

Los astrónomos Hiparco y Ptolomeo mejoraron el sistema cartográfico, que hasta Ptolomeo en el siglo II a. C. consistía en trazar un cuadriculado de líneas de latitud y longitud sobre el mapa. Esto funciona para regiones pequeñas de la Tierra, pero no para grandes distancias. Ptolomeo resolvió el problema mapeando los círculos de meridianos y de latitud (sobre la esfera de la Tierra) como líneas curvas en el plano del mapa.

Como quiera que sea, es evidente que desde la antigüedad clásica ya existían métodos para poder asignarles dos coordenadas a los puntos sobre una superficie, en este caso la superficie de la Tierra. Hacerlo de manera más general tomó siglos en las matemáticas.

Se atribuye la introducción de los ejes de coordenadas en las matemáticas a dos franceses, al matemático Pierre de Fermat y al filósofo René Descartes. Para abordar problemas geométricos lo que ambos hacían era trazar una línea de referencia (que hoy sería el eje “x”), con un punto de origen.

Las distancias de los puntos en el plano se medían a lo largo de ese eje para “x” y a lo largo de una línea auxiliar que intersecaba al eje “x”. Es decir, lo que hoy llamamos el eje “y” no necesitaba ser perpendicular al eje de las equis. Para cada problema particular se trazaba el segundo eje de la manera más apropiada para resolver el problema en cuestión. O no se le trazaba explícitamente, y las distancias al eje “x” se medían a lo largo de una dirección que quedaba implícita pero no dibujada.

Descartes utiliza esta técnica en su “Geometría” de 1637, un apéndice matemático de su opus magnum, “El Discurso del Método”. Se considera a la Geometría de Descartes como el texto que instauró la llamada “geometría análitica”, es decir, aquella que no opera con regla y compás, sino con ecuaciones.

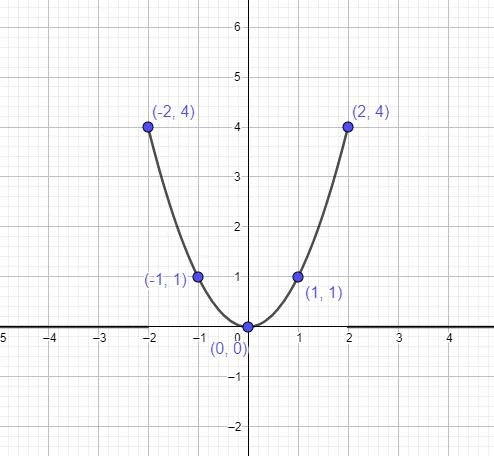
Ya con un sistema de referencia cartesiano es posible hablar de la gráfica de una función, por ejemplo, la función cuadrática . La imagen de esta función es una curva llamada parábola. Utilizando la función, cada valor de “x” obtenemos uno de “y” y los puntos (x,y) los vamos graficando de acuerdo con los ejes cartesianos, como indica la figura.

Es importante recalcar que Descartes no utilizaba dos ejes perpendiculares, sino ejes muchas veces no ortogonales, según el problema. Se ha tratado de rastrear cuándo se llegó a dibujar funciones utilizando la forma  de ejes perpendiculares hoy tan útil. Se ha dicho que esto fue una contribución de Frans van Schooten, un holandés comentarista de Descartes y que tradujo la Geometría del francés al latín (para que pudiera ser leída por los eruditos europeos). Se ha mencionado también a otro holandés, Jan de Witt, que en su libro Elementa Curvarum Linearum habría dado ese paso. Sin embargo, el libro en cuestión prácticamente no contiene diagramas y, cuando los tiene, se asemejan mucho a los de Descartes.

El historiador de la ciencia Carl Boyer menciona en su Historia de la Geometría Analítica que el primero que comenzó a utilizar dos ejes ortogonales o perpendiculares de manera sistemática fue el célebre Isaac Newton. Esto ocurrió en un texto que publicó como apéndice de su Óptica de 1704, pero que ya había redactado desde 1676, o sea cuarenta años después de la Geometría de Descartes. Utilizando un sistema de coordenadas como el moderno, Newton pudo presentar las gráficas de diferentes tipos de funciones cúbicas, demostrando plásticamente la conexión entre el álgebra y la geometría. Además, Newton utilizaba coordenadas positivas y negativas, dibujando las curvas en los cuatro cuadrantes del plano cartesiano. Descartes, por el contrario, había eludido las coordenadas negativas, manteniéndose solamente en el primer cuadrante del plano cartesiano, por así decirlo.

De manera que tomó casi 19 siglos, desde Ptolomeo hasta Newton, para que los matemáticos se decidieran, de una vez por todas, a considerar puntos en el plano como pares de dos mediciones respecto a dos ejes de coordenadas.

En el camino hubo muchas dificultades. La primera de ellas era el escaso desarrollo de los métodos algebraicos para resolver ecuaciones, comparados con los refinados métodos geométricos de Euclides. El mismo Newton resuelve problemas de atracción gravitatoria en su opus magnum, Principia Mathematica, de manera geométrica, siguiendo a Euclides, y no de manera algebraica. Aparentemente Newton pensaba que las demostraciones euclidianas serían más comprensibles para los lectores.

Hoy hablamos de los “ejes cartesianos”, del “plano cartesiano”, de “coordenadas cartesianas”, recordando al filósofo Descartes, aquel que dudó de todo para poder dejar de dudar. La geometría analítica, basada en manipular las coordenadas cartesianas para encontrar ecuaciones que definen curvas, o para resolver problemas geométricos, es una de las bases de la educación superior y una herramienta imprescindible de los matemáticos. Y aunque hoy la idea se nos antoja trivial, la verdad es que tomó siglos llegar a la geometría analítica con sus ejes cartesianos canónicos.