Si queremos definir qué es un número, hay varias alternativas posibles. Una es la asociada con el nombre del matemático y filósofo británico Bertrand Russell; fácil de comprender pero requiere que podamos concebir conjuntos infinitos.

La idea de Russel es que, si tengo dos conjuntos y puedo poner en correspondencia los elementos de uno de ellos con los del segundo, entonces decimos que los conjuntos contienen el mismo número de elementos. En la figura los dos conjuntos tienen tres elementos y las líneas rojas muestran la correspondencia entre los elementos de cada conjunto.

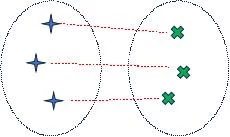
Ahora bien, hay muchos conjuntos de tres elementos, una infinidad de ellos. Podemos pensar en tres manzanas, tres cruces, tres zapatos, etc. Pero todos son equivalentes entre sí porque siempre es posible establecer la correspondencia entre sus tres elementos, como en la figura anterior. El conjunto de todos esos conjuntos de tres elementos es lo que se llama su “clase de equivalencia”.

Lo interesante es que hay una clase de equivalencia para los conjuntos con un elemento, otra para los que contienen dos elementos, otra para tres, y así sucesivamente.

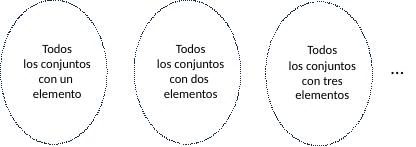
Entonces les ponemos nombre: a la clase de equivalencia de todos los conjuntos con un elemento la llamamos “1”, a la de conjuntos con dos elementos la llamamos “2” y así sucesivamente.

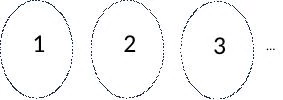
Eso es todo, para comenzar. Si alguien me pregunta qué es número uno le respondo, la clase de equivalencia de todos los conjuntos que son equivalentes al conjunto {a} que contiene una sola letra. El dos es la clase de equivalencia de todos los conjuntos que pueden ser puestos en correspondencia con el conjunto {a,b}, para mostrar un conjunto con dos elementos. Y así sucesivamente.

Esta definición, en la que los números son el nombre de conjuntos infinitos donde hemos capturado todos los conjuntos con el mismo número de elementos pareciera ser algo ociosa, innecesariamente complicada. Sin embargo, tiene la gran virtud: de esta definición es posible pasar a las operaciones aritméticas.

Si queremos saber cuánto es 1+1, tomamos todos los conjuntos contenidos en la clase de equivalencia 1 y los unimos, uno por uno, con cada conjunto en la misma clase. La unión de dos conjuntos de un elemento nos da un conjunto de dos elementos, siempre. No hay conjunto de dos elementos que no pueda ser generado así, uniendo dos conjuntos de un elemento. Eso quiere decir entonces que 1+1=2. De manera similar se puede interpretar cualquier otra adición de números. Con la teoría de conjuntos la operación de adición es fácil de definir y lo mismo sucede con la substracción.

En realidad, Russell resucitó una definición que había formulado el matemático alemán Gottlob Frege casi veinte años antes que él. Frege llama a la posibilidad de poner un conjunto en correspondencia “uno-a-uno” con los elementos de otro conjunto la relación de “equi-numerosidad” (igual número de elementos). Partiendo de esa relación se construyen las clases de equivalencia explicadas arriba.

Si no se quiere usar como referencia para los conjuntos de un elemento, o dos, conjuntos empíricos, tomados del mundo, se pueden construir conjuntos de varios elementos de manera puramente lógica. Para hacer eso se comienza con el conjunto vacío . Este conjunto tiene cero elementos. Un conjunto con un elemento puede ser 1= { Es decir, este es conjunto con el elemento único  Un conjunto de dos elementos sería 2= {, y así sucesivamente.

De esta manera la definición de un número se convierte en un problema puramente lógico.