En nuestro día a día tenemos que medir distancias. Si viajamos a otra ciudad nos interesa saber a cuántos kilómetros se encuentra de nuestro punto de partida; se puede medir esa distancia si consideramos la línea recta que las une y estimamos su longitud (como si la Tierra fuera plana). Esto es lo que se llama la “distancia euclidiana”, en honor al gran geómetra Euclides de Alejandría.

Ahora bien, hay otras formas de medir distancias. Los matemáticos las llaman “métricas” y un ejemplo sería contar el número de cuadras o manzanas que tenemos que recorrer si transitamos en una ciudad con todas las calles dispuestas como en una cuadrícula.

En el diagrama abajo podemos ver el camino que se puede seguir para ir del punto A al punto B en una ciudad así dispuesta. Necesitamos recorrer 12 lados de manzanas para ir de A a B (línea azul). Si utilizamos el recorrido rojo también recorremos 12 lados de manzanas, y lo mismo por el recorrido amarillo. Como se puede ver, con la métrica de Manhattan hay muchos caminos alternativos que arrojan la misma distancia recorrida. La línea verde muestra la distancia euclidiana, que en esta ciudad no puede utilizar un transeúnte (sólo un dron).

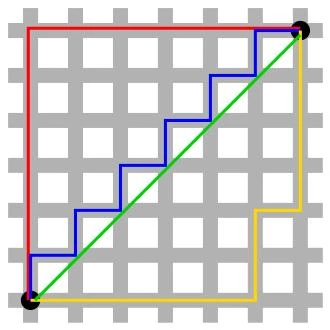
Figura 1. Métrica de Manhattan vs métrica euclidiana (ilustración: Wikipedia)

Todo esto es intuitivo, pero los matemáticos se preguntan si al medir distancias de esta manera pudiera ser que se obtuvieran resultados paradójicos. Por eso, una métrica digna de su nombre debe satisfacer cuatro condiciones:

Primera: La distancia entre un punto A y el mismo debe ser cero. La métrica de Manhattan satisface esta propiedad. Para ir de A a A nos quedamos parados.

Segunda: La distancia entre dos puntos debe ser positiva. Es decir, en la métrica de Manhattan sólo acumulamos las calles que recorremos, pero nunca las restamos.

Tercera: La distancia de A a B es la misma que la distancia de B a A. Esto quiere decir que podemos hacer el recorrido de regreso, por las mismas calles, y la distancia que midamos será la misma. En la figura es obvio que el recorrido azul se puede utilizar de ida y vuelta.

Cuarta: Y un punto muy importante: para ir de A a B podemos pasar por Z, es decir vamos de A a Z, y después de Z a B, pero la distancia total con este rodeo no puede ser menor que la distancia entre A y B. Esto es lo que se llama la “desigualdad del triángulo” que básicamente dice que la suma de dos lados de un triángulo no puede ser menor que la longitud del lado más grande. No podemos dar un rodeo en una ciudad y esperar que el recorrido sea más corto que al tratar de ir de la forma más directa posible.

Como vemos, lo interesante de la métrica de Manhattan es que hay caminos alternativos con la misma longitud total, lo que no ocurre con la métrica euclidiana. En ésta última la línea recta que conecta dos puntos es el camino de mínima distancia. La métrica de Manhattan es la métrica relevante para un chofer de taxi que tiene que recorrer las calles siguiendo el cuadriculado de la ciudad.

Un ejemplo de una forma de medir distancias, que no es una métrica, es contar el número de calles que recorremos al ir de A a B, como antes, pero si algunas calles tienen un sólo sentido quiere decir que para regresar de B a A no podemos simplemente tomar el mismo camino en sentido inverso.

Cualquiera que ha manejado un auto está consciente de este problema. Una métrica de Manhattan en una ciudad con calles de un sólo sentido no es realmente una métrica, no cumple el tercer requisito arriba planteado ya que la distancia de A a B puede ser distinta a la distancia al ir de B a A, por los rodeos que hay que hacer a veces.

Los matemáticos no serían matemáticos si no trataran de definir formas de medir distancia que son contraintuitivas, pero que satisfacen la definición. Es una forma de poner a prueba la teoría y ver hasta dónde nos puede llevar.

Una “métrica discreta” asigna el valor cero a la distancia de un punto A a sí mismo, y el valor 1 cuando vamos de A a cualquier otro punto B, distinto de A. Es ésta una métrica porque los valores son positivos (segunda condición) y se satisfacen las condiciones uno, tres y cuatro, como el lector puede constatar.

Por ejemplo, si vamos de A a Z y de Z a B, la distancia total recorrida es 1+1, que es mayor que la distancia de A a B (uno). Se cumple la desigualdad del triángulo. Esta métrica tan extraña es a veces llamada una métrica “degenerada”, ya que lleva la definición al extremo. Y si se quiere, otra métrica aún más extraña es asignarle la distancia cero a cualquier longitud entre dos puntos. Una definición tal satisface las condiciones de una métrica, aunque no sea muy útil.

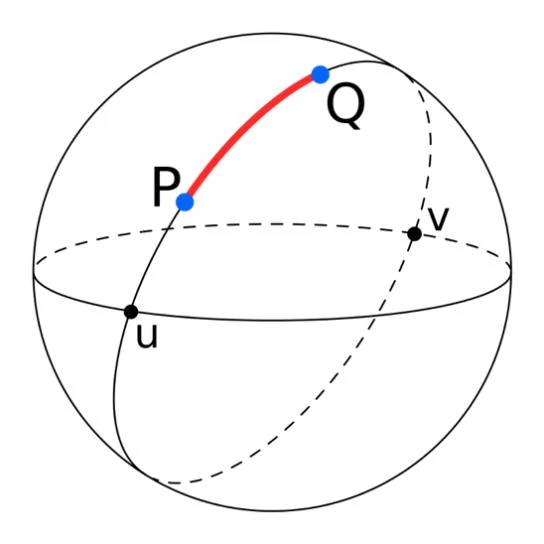
Figura 2. Distancia del punto P al punto Q sobre una esfera (ilustración: Wikipedia)

Más interesantes son las métricas sobre esferas, por ejemplo, para ir sobre la Tierra de un punto P a un punto Q. La distancia más corta se obtiene cortando la esfera terrestre con un cuchillo, pasando el corte por P y Q, además del centro de la esfera. La distancia es la del máximo arco circular que une los dos puntos P y Q sin abandonar la esfera (ya que vamos sobre su superficie). Es fácil ver que esta definición de distancia cumple las cuatro condiciones de una métrica.

Hay superficies más complejas que la de una esfera y es un problema matemático encontrar la manera de medir la distancia más corta entre dos puntos sobre esas superficies. Es lo que se llama una “geodésica” y existe toda una industria matemática para encontrar geodésicas en superficies arbitrarias, un problema que es de interés por sus implicaciones para la física moderna.