El tema de los diputados y senadores plurinominales resulta polémico (por decir lo menos), y suele abordarse en múltiples conversaciones ocasionales, que pueden convertirse en apasionadas discusiones con posiciones antagónicas. Es muy común que una de las partes enfrentadas se manifieste fuertemente a favor de eliminar a todos los plurinominales. Por lo regular, dicha posición se defiende sobre la base de lo que le cuesta al país cada diputado; no solamente los plurinominales.

Si ponemos atención en las diversas opiniones que hay en el ambiente sobre los ‘pluris’, se puede constatar que pocas veces se explica la razón de fondo que hay para mantenerlos en una ley electoral. Y es que con ellos deberíamos acercarnos tanto como sea posible al objetivo ideal que debería observarse en una cámara de representantes, de acuerdo con lo que la ciudadanía ha manifestado al votar, es decir, a la proporción o porcentaje de votos que cada partido recibió el día de las elecciones.

La ley electoral vigente en México dice que la cámara de diputados se integrará por 300 representantes de los partidos que hayan ganado por mayoría relativa de votos en los 300 distritos electorales en los que el país está dividido, y por 200 diputados plurinominales más, que se distribuirán —según el método de repartición plasmado en la ley— entre todos los partidos que participaron en la jornada electoral.

En un mundo ideal, regido bajo esquemas lógicos y justos, la repartición de ‘pluris’ que marca la ley debería garantizar que se alcance ese objetivo. Lo que pretendemos explicar aquí no es cómo se asignan los ‘pluris’ según la ley electoral vigente, sino su razón de ser sobre una base lógica y presumiblemente justa.

Vamos a suponer que, después de saber qué partidos ganaron por mayoría absoluta en cada uno de los 300 distritos electorales, se cuenta con un número P de diputados plurinominales para ser repartidos entre los partidos políticos. El número total de diputados en la cámara es de 300 + P. En México P=200, por lo que tomaremos igual a 500 el número total de diputados en la cámara.

Ahora, supongamos que uno de los partidos obtuvo un total de v (v minúscula) votos a su favor. Si V (V mayúscula) fue el total de votos válidos registrados el día de la jornada electoral en todo el país, entonces la proporción de votos recibida por este partido es el resultado de dividir v entre V, lo cual escribimos como la fracción v/V.

¿Cuál es la razón de fondo para mantener los plurinominales en la ley electoral?

El porcentaje de votos recibido por dicho partido se obtiene multiplicando la fracción v/V por 100. La suma de todos los diputados que ganaron por mayoría absoluta en sus respectivos distritos y que pertenecen a este mismo partido político es igual a m (m minúscula). El objetivo ideal planteado en el segundo párrafo de este escrito se obtendría si el número p (p minúscula) de los ‘pluris’ que se sumarían a los m diputados, que ya tiene asegurados este partido, hace que la proporción (m + p)/500 de diputados que tendría el partido en la cámara, fuera lo más cercana posible a la proporción (fracción) v/V de votos que obtuvo.

Bajo este supuesto, para determinar el número p de ‘pluris’ que le tocarían a cada partido se pueden seguir los siguientes pasos:

a) Para cada partido se hace una regla de tres: “500 es a V, como x es a v”, con lo cual se obtiene que x es igual a 500 × (v/V).

b) A este número se le restan los diputados de mayoría que el partido obtuvo y el resultado se redondea para obtener un número entero.

Esto lo indicamos escribiendo p = Redondeo{500 × (v/V) – m}. El redondeo es necesario porque la fracción v/V no es un número entero y la ley electoral tendría que especificar cuál será el método de redondeo a aplicar.

Nuestros compañeros Jean Bernard Hayet y Johan Van Horebeek ilustran en su contribución a este mismo número, algunos de los métodos más usados en la práctica. Al final, la suma de todos los números p, (que son los ‘pluris’ asignados a cada partido según el objetivo ideal), debería ser igual a 200.

Sin embargo, es posible que al hacer las operaciones, algunos de los números 500 × (v/V) – m resulten ser negativos. Esto sucede cuando en un partido, la fracción v/V de votos que recibió es estrictamente menor que la fracción m/500 de diputados con los que estaría presente en la cámara, en virtud de sus diputados ganados en los distritos. Esto significa que esos partidos ya están sobrerrepresentados en la cámara con tan solo sus diputados de distrito. La lógica y el sentido común nos dicen entonces que a esos partidos ya no habría por qué asignarles ‘pluris’.

Esos ‘pluris’ no asignados a los partidos ya sobrerrepresentados podrían ser asignados a partidos políticos que, aún sin haber ganado una sola diputación por mayoría absoluta de votos, hayan alcanzado una proporción mínima v/V que la ley determine para permitirles tener una representación proporcional en la cámara, cosa que de hecho ocurre en la ley mexicana vigente.

Por lo pronto, el método se puede emplear como “laboratorio para experimentar” con los resultados observados en las pasadas elecciones intermedias del año 2021 y obtener los resultados mostrados en la Tabla 1.

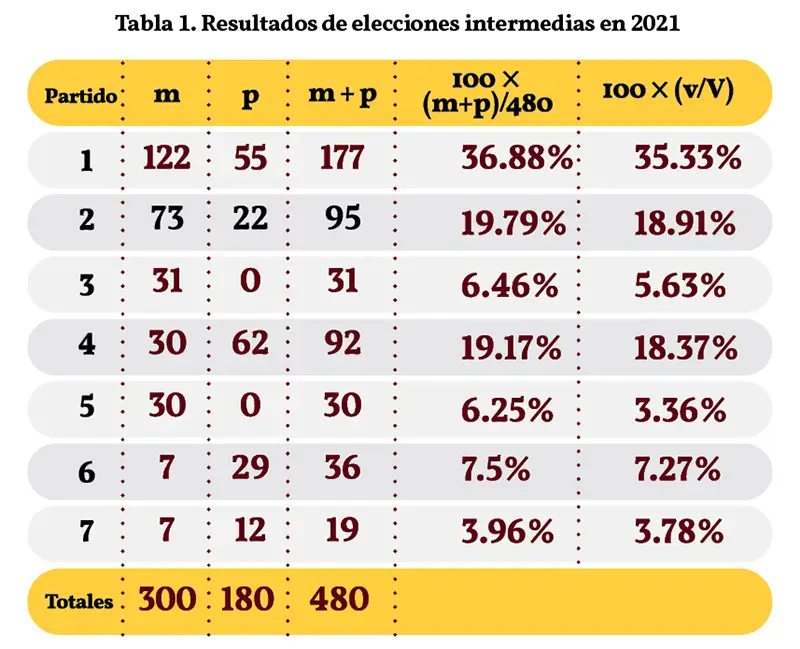
Fuentes: https://computos2021.ine.mx/votos-ppyci/grafica
https://es.wikipedia.org/wiki/Elecciones_federales_de_México_de_2021

Con el fin de mantener el ejemplo en los términos más simples posibles, no se han tomado en cuenta los votos a candidatos independientes ni los votos inválidos. Tampoco se han tomado en cuenta los resultados obtenidos por los partidos que no ganaron diputación alguna por mayoría absoluta, ni los que obtuvieron menos de 1.5 millones de votos.

Bajo estas simplificaciones y con el criterio de redondear al número entero más cercano, los resultados de las fuentes citadas nos permiten comprobar que hay dos partidos para los que sus números p resultaron negativos: los partidos “3” y “5”, lo que traducimos en ambos casos como una asignación de 0 ‘pluris’ para ellos. Es interesante notar en este ejemplo que ninguno de estos dos partidos coincide con los dos partidos que más diputaciones ganó por mayoría. El número P de plurinominales necesarios, para equilibrar la representación proporcional, puede bajar incluso de 200 a 180 como indican los totales mostrados y se obtiene una muy buena aproximación de las últimas dos columnas.

En un mundo ideal con esquemas justos, la repartición de ‘pluris’ debe hacerse de acuerdo con lo que la ciudadanía manifiesta al votar.

Algunas conclusiones derivadas de la distribución de ‘pluris’ expuesta de acuerdo con principios ideales y mecanismos lógicos serían las siguientes:

1) Puede ser que no se necesiten tantos como 200 ‘pluris’ para alcanzar una representación proporcional suficientemente justa en la cámara de diputados pero, igualmente, podría ser que se necesitaran más. Una ley electoral idealmente realista podría buscar un modelo alternativo en el que al número P de ‘pluris’ a repartir se le permitiera variar entre un valor mínimo y uno máximo, de acuerdo con análisis estadísticos de los resultados observados en un número grande de elecciones anteriores.

2) Al aumentar el número de distritos electorales (la suma de los números m de diputados ganadores por mayoría absoluta), aumenta también, y puede ser que muy significativamente, la suma de todos los ‘pluris’.

3) Se pueden incluir fácilmente reglas que, por diversas razones, se consideren necesarias como, por ejemplo, que partidos con pocos votos obtenidos puedan recibir ‘pluris’ a partir de un cierto porcentaje mínimo.

4) El método expuesto responde en buena medida al espíritu que menciona la matemática Eugenia Cheng en su libro How to bake π (Cómo cocinar a π), refiriéndose a lo que hacen las matemáticas para nosotros y de lo que ellas tratan: maths is the [logical] study of how logical things work (las matemáticas son el estudio [lógico] de cómo funcionan las cosas lógicas).