Antes de las elecciones tenemos las encuestas. La opinión pública y preferencia electoral son monitoreadas a través de diferentes herramientas, entre las que se encuentran las encuestas, que se llevan a cabo mediante una recopilación de muestra aleatoria y representativa del total de personas de las cuales se quiera conocer sus preferencias, ideas, o reflexiones.

Las encuestas permiten que no sea necesario que se conozca la opinión de todas y cada una de las personas en una población, tal y como la mide un censo, sino que basta con una porción para inferir de esa muestra, con cierta probabilidad, el comportamiento de la población total. Poniéndolo en otros términos, no es necesario analizar toda la sangre de una persona para conocer su tipo, su composición y si tiene o no alguna enfermedad. Basta con analizar una muestra.

La realización de un censo cuesta dinero y tiempo. Sin embargo, mediante la selección aleatoria de una muestra representativa de la población se puede obtener información sobre las características y comportamientos del conjunto. Obtener muestras para deducir, mediante la inferencia estadística, el comportamiento de la población ahorra recursos y posibilita una toma de decisiones más eficiente y precisa en diversos ámbitos, desde políticas públicas hasta estrategias comerciales.

La opinión pública y preferencia electoral son monitoreadas a través de diferentes herramientas.

El comportamiento de la población se infiere a través de dos tipos de medidas de interés de la muestra: de tendencia central (la media o promedio) y de dispersión (varianza y desviación estándar). Las medidas de tendencia central tienden a converger con alta probabilidad en las de la población (por ejemplo, la preferencia por un partido), dado que la muestra, al ser aleatoria, garantiza que cada persona tenga la misma probabilidad de ser seleccionada. Para obtener buenos resultados, la muestra debe tener el tamaño “apropiado”.

La inferencia estadística se fundamenta en el llamado teorema del límite central (TLC), el cual afirma que, a medida que se incrementa el tamaño de la muestra, la media muestral tiende a aproximarse, cada vez más, a la media poblacional. Más aún, el promedio de las medias de todas las muestras teóricamente posibles es igual a la media poblacional.

De acuerdo con el TLC, la media de una muestra aleatoria es el mejor estimador de la media poblacional. Además, se puede construir un intervalo de confianza alrededor de un valor muestral (estadística o estadístico), lo que permite calcular el nivel de confianza en el que se espera que dicho intervalo contenga al valor poblacional.

Obtener muestras para deducir, mediante la inferencia estadística, el comportamiento de la población ahorra recursos.

Por ejemplo, si estamos midiendo la preferencia electoral por un candidato (en porcentaje de la población) un intervalo con nivel de confianza al 95 por ciento implica que, si se levantaran 100 muestras de la población, se espera que en 95 de ellas la preferencia electoral de toda la población esté contenida dentro del intervalo de confianza. Se dice, por ejemplo, “la preferencia por el partido A es de 30 por ciento con un margen de 2 por ciento de error, con 95 por ciento de confianza”.

La inferencia estadística permite conocer los valores poblacionales (parámetros) al conocer los valores muestrales (estadística o estadístico) de las medidas de tendencia central, ya sea puntualmente o a través de intervalos; además brinda la oportunidad de comprobar si la relación observada entre dos variables en la muestra existe realmente en la población.

La forma en que se plantea la pregunta básica de la inferencia es la siguiente: ¿cuál es la probabilidad de que una relación postulada entre dos variables de la muestra no exista en la población? Por ejemplo, queremos saber si una candidata A realmente tiene mayor preferencia electoral que una candidata B.

Supongamos que una encuesta muestra que la candidata A obtiene 48 por ciento de preferencia, mientras que la candidata B obtiene el 33 por ciento. Si la encuesta tiene un margen de error de +/- tres puntos porcentuales, entonces los valores estadísticos deberán estar dentro de ese intervalo: únicamente podemos afirmar que la preferencia por la candidata A iría de 45 a 51 por ciento, mientras que la preferencia por la candidata B iría de 30 a 36 por ciento. En este caso, los intervalos de confianza no se traslapan y tenemos alta confianza en que la candidata A ganará las elecciones.

Podemos obtener estimaciones sobre las características y comportamientos de una población a partir de muestras aleatorias.

En otro caso, si la encuesta muestra que la candidata A obtiene 42 por ciento de preferencia, mientras que la candidata B obtiene 37 por ciento, con un mismo margen de error de +/- tres puntos porcentuales, entonces la preferencia por la candidata A iría de 39 a 45 por ciento, mientras que la preferencia por la candidata B iría de 34 a 40 por ciento. En este caso, dado que los intervalos de las preferencias de las candidatas se traslapan, se dice que existe un empate técnico entre ambas.

En la estadística existen las fórmulas necesarias para calcular los márgenes de error de encuestas: en general, mientras mayor es el tamaño de la muestra, más pequeño es el margen de error o  intervalo de confianza. En muchas encuestas electorales se trata de incluir al menos mil personas, además distribuidas por todo el país y representativas del género y edades de los votantes.

En encuestas bien diseñadas, los resultados se aproximan a los parámetros poblacionales. Las preferencias electorales, la aprobación de actores políticos y la opinión a favor o en contra de ciertos temas, entre otros, son los mismos, dentro de un margen de error, que los que se observan en la población.

En resumen, a través de la inferencia estadística, basada en el teorema del límite central, podemos obtener estimaciones sobre las características y comportamientos de una población a partir de muestras aleatorias y, por tanto, representativas. Mientras mayor es el tamaño de la muestra menor es el margen de error, que debe ser considerado al interpretar los resultados. La estadística proporciona un marco científico para la investigación y el análisis de datos, permitiendo una comprensión más profunda de la sociedad y facilitando la toma de decisiones.

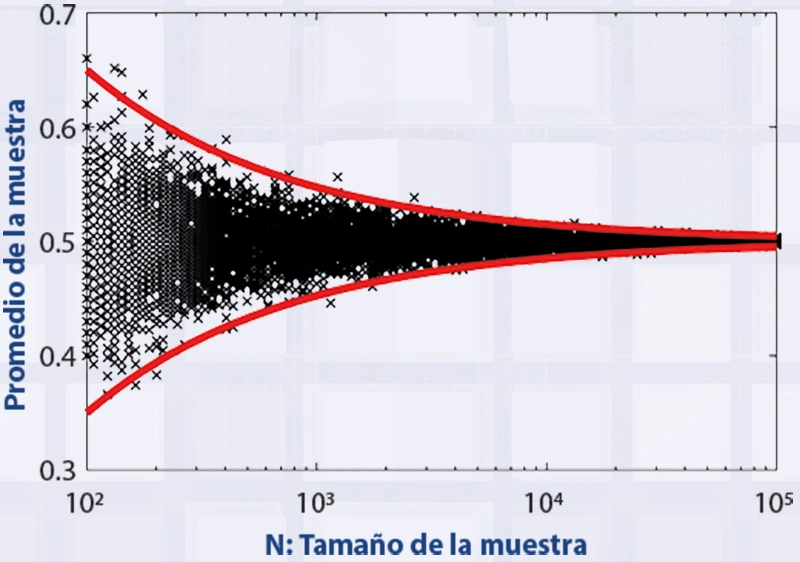
La gráfica ilustra el teorema del límite central para un experimento en el que se lanza una moneda al aire. Esperamos que el promedio de “águilas” sea del 50%, pero si realizamos cien repeticiones, el promedio oscila entre un poco menos de 40% y un poco más de 60%. A medida que aumenta el tamaño de la muestra (N, eje horizontal) se va cerrando el margen de error (líneas rojas) y el promedio de la muestra se acerca cada vez más a 50%.